Alaa Maalouf
alaam_at_mit_dot_edu

|
CV |
Google Scholar |
LinkedIn|
|
Github |
Twitter |
|
I'm the Neubauer Assistant Professor of Computer Science at the University of Haifa. I am also a Research Affiliate at MIT CSAIL, and an Associate at Harvard SEAS.
My research spans machine learning, robotics, and AI-driven scientific discovery. Specifically, I focus on:
(i) making machine learning more efficient to democratize its access and expand its applicability,
(ii) developing intelligent robots capable of reasoning, interacting, and making decisions akin to humans, and
(iii) leveraging machine learning and robotics to drive scientific discovery. Thus, I'm also a Principal Investigator at Project CETI, where I explore the intersection of AI and real-world impact—working to decode and translate the language of sperm whales.
Previously, I was a postdoctoral researcher at MIT CSAIL, working with
Prof. Daniela Rus, and before that I received my Ph.D. from the Department of Computer Science at the University of Haifa , where I was supervised by Prof. Dan Feldman.
|
Present Experience

Haifa University
Assistant Professor
Mar 25 - Present
|

CSAIL MIT
Research Affiliate
Apr 25 - Present
|

Harvard
Associate
Mar 25 - Present
|

CETI
ML PI
Mar 25 - Present
|
Previous Experience

CSAIL MIT
Postdoc
Jan 23 - Mar 25
|

Harvard
Postdoc Associate
Mar 23 - Mar 25
|

CETI
ML Researcher
Feb 23 - Mar 25
|

DataHeroes
Lead ML Researcher
Aug 22 - Jan 23
|

Mellanox (NVIDIA)
Chip Design
Mar 15 - Nov 19
|

Haifa University
M.Sc. + Ph.D. in CS
Oct 16 - Sep 19, Mar 20 - July 22
|
| Teaching @ University of Haifa |
2021-2022: Head TA, Machine Learning
2021-2022: Head TA, Deep Learning
2019-2020: TA, Learning Big Data in the Cloud
2018-2019: Head TA, Deep Learning
2018-2021: Advisor, Robotics and Big Data Lab
| 2024 |
|
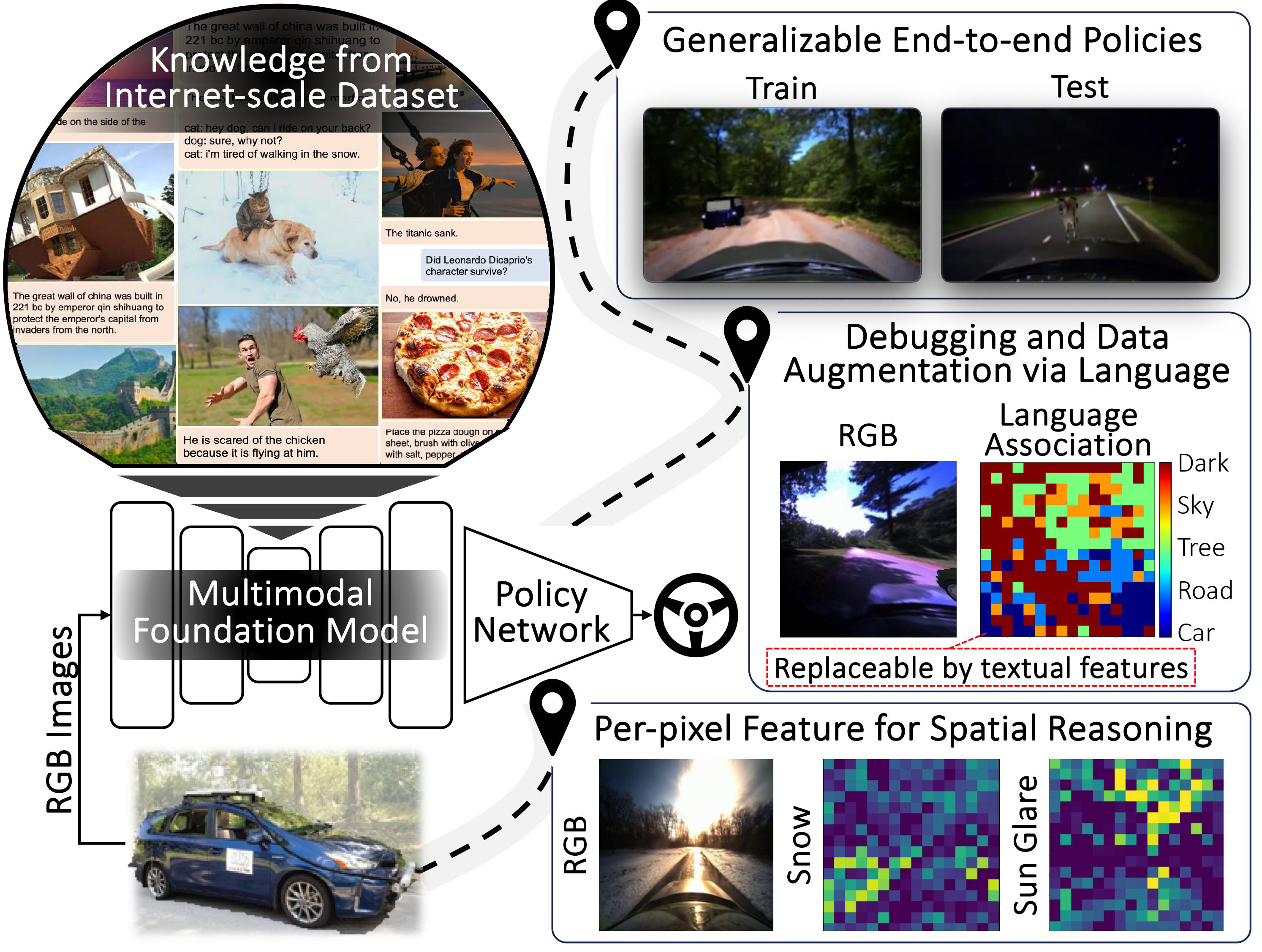
Drive Anywhere: Generalizable End-to-end Autonomous Driving with Multi-modal Foundation Models
Tsun-Hsuan Wang, Alaa Maalouf, Wei Xiao, Yutong Ban, Alexander Amini, Guy Rosman, Sertac Karaman, Daniela Rus
ICRA 2024
paper |
abstract |
bibtex |
code and webpage |
video
As autonomous driving technology matures, end-to-end methodologies have emerged as a leading strategy, promising seamless integration from perception to control via deep learning. However, existing systems grapple with challenges such as unexpected open set environments and the complexity of black-box models. At the same time, the evolution of deep learning introduces larger, multimodal foundational models, offering multi-modal visual and textual understanding. In this paper, we harness these multimodal foundation models to enhance the robustness and adaptability of autonomous driving systems, enabling out-of-distribution, end-to-end, multimodal, and more explainable autonomy. Specifically, we present an approach to apply end-to-end open-set (any environment/scene) autonomous driving that is capable of providing driving decisions from representations queryable by image and text. To do so, we introduce a method to extract nuanced spatial (pixel/patch-aligned) features from transformers to enable the encapsulation of both spatial and semantic features. Our approach (i) demonstrates unparalleled results in diverse tests while achieving significantly greater robustness in out-of-distribution situations, and (ii) allows the incorporation of latent space simulation (via text) for improved training (data augmentation via text) and policy debugging.
@article{wang2023drive,
title={Drive anywhere: Generalizable end-to-end autonomous driving with multi-modal foundation models},
author={Wang, Tsun-Hsuan and Maalouf, Alaa and Xiao, Wei and Ban, Yutong and Amini, Alexander and Rosman, Guy and Karaman, Sertac and Rus, Daniela},
journal={arXiv preprint arXiv:2310.17642},
year={2023}
}
|
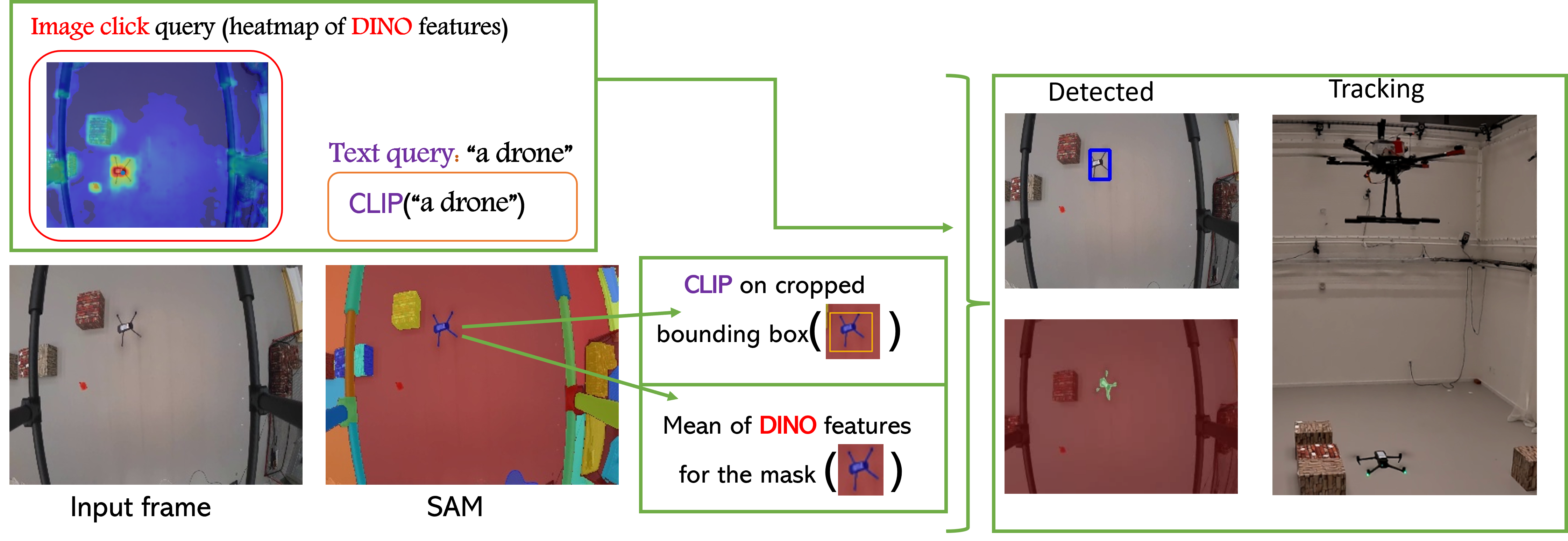
Follow Anything: Open-set detection, tracking, and following in real-time
Alaa Maalouf, Ninad Jadhav, Krishna Murthy Jatavallabhula, Makram Chahine, Daniel M.Vogt, Robert J. Wood, Antonio Torralba, Daniela Rus
RA-L 2024
paper |
abstract |
bibtex |
code and webpage |
video
Tracking and following objects of interest is critical to several robotics use cases, ranging from industrial automation to logistics and warehousing, to healthcare and security. In this paper, we present a robotic system to detect, track, and follow any object in real-time. Our approach, dubbed ``follow anything'' (FAn), is an open-vocabulary and multimodal model -- it is not restricted to concepts seen at training time and can be applied to novel classes at inference time using text, images, or click queries. Leveraging rich visual descriptors from large-scale pre-trained models (foundation models), FAn can detect and segment objects by matching multimodal queries (text, images, clicks) against an input image sequence. These detected and segmented objects are tracked across image frames, all while accounting for occlusion and object re-emergence. We demonstrate FAn on a real-world robotic system (a micro aerial vehicle) and report its ability to seamlessly follow the objects of interest in a real-time control loop. FAn can be deployed on a laptop with a lightweight (6-8 GB) graphics card, achieving a throughput of 6-20 frames per second. To enable rapid adoption, deployment, and extensibility, we open-source all our code on our project webpage.
@ARTICLE{maalouf2024follow,
author={Maalouf, Alaa and Jadhav, Ninad and Jatavallabhula, Krishna Murthy and Chahine, Makram and Vogt, Daniel M. and Wood, Robert J. and Torralba, Antonio and Rus, Daniela},
journal={IEEE Robotics and Automation Letters},
title={Follow Anything: Open-Set Detection, Tracking, and Following in Real-Time},
year={2024},
volume={9},
number={4},
pages={3283-3290},
keywords={Robots;Feature extraction;Real-time systems;Fans;Streaming media;Whales;Task analysis;AI-enabled robotics;object detection;segmentation and categorization;semantic scene understanding},
doi={10.1109/LRA.2024.3366013}}
|
| 2023 |
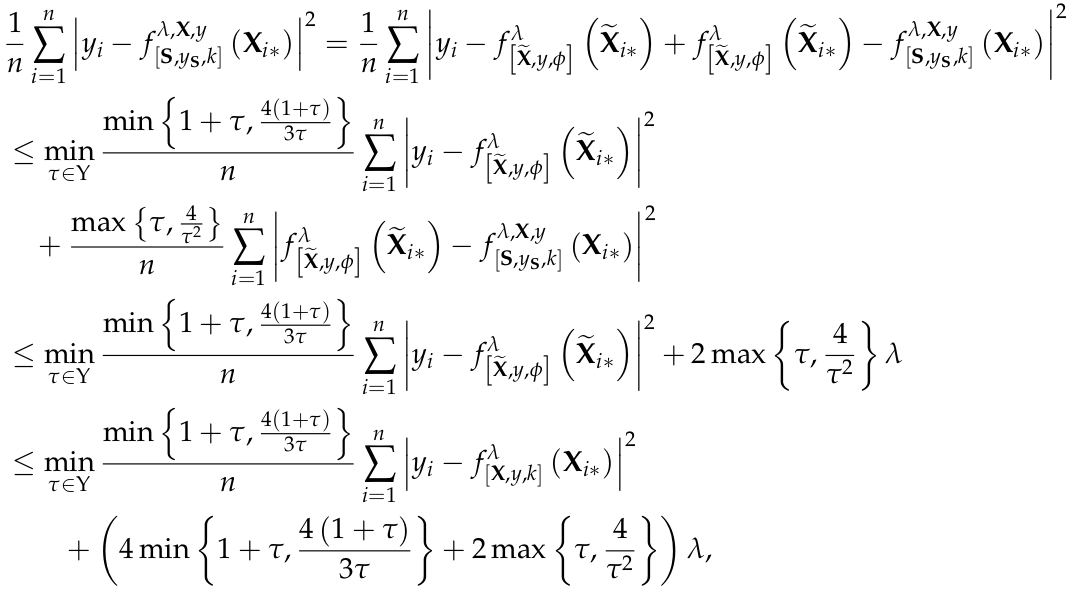
|
On the Size and Approximation Error of Distilled Sets
Alaa Maalouf, Murad Tukan, Noel Loo, Ramin Hasani, Mathias Lechner, Daniela Rus
NeurIPS 2023
paper |
abstract |
bibtex
Dataset Distillation is the task of synthesizing small datasets from large ones while still retaining comparable predictive accuracy to the original uncompressed dataset. Despite significant empirical progress in recent years, there is little understanding of the theoretical limitations/guarantees of dataset distillation, specifically, what excess risk is achieved by distillation compared to the original dataset, and how large are distilled datasets? In this work, we take a theoretical view on kernel ridge regression (KRR) based methods of dataset distillation such as Kernel Inducing Points. By transforming ridge regression in random Fourier features (RFF) space, we provide the first proof of the existence of small (size) distilled datasets and their corresponding excess risk for shift-invariant kernels. We prove that a small set of instances exists in the original input space such that its solution in the RFF space coincides with the solution of the original data. We further show that a KRR solution can be generated using this distilled set of instances which gives an approximation towards the KRR solution optimized on the full input data. The size of this set is linear in the dimension of the RFF space of the input set or alternatively near linear in the number of effective degrees of freedom, which is a function of the kernel, number of datapoints, and the regularization parameter λ. The error bound of this distilled set is also a function of λ. We verify our bounds analytically and empirically.
@article{maalouf2023size,
title={On the Size and Approximation Error of Distilled Sets},
author={Maalouf, Alaa and Tukan, Murad and Loo, Noel and
Hasani, Ramin and Lechner, Mathias and Rus, Daniela},
journal={arXiv preprint arXiv:2305.14113},
year={2023}
}
|
|
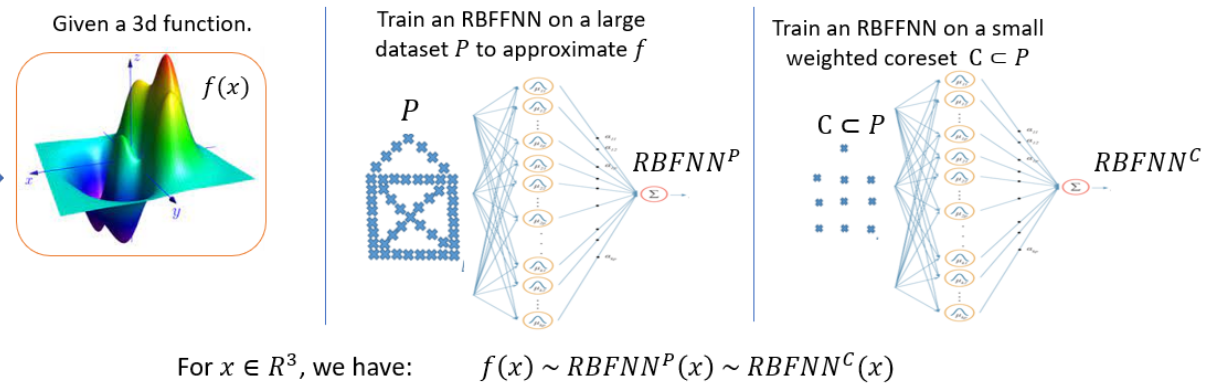
Provable Data Subset Selection For Efficient Neural Networks Training
Murad Tukan, Samson Zhou, Alaa Maalouf, Daniela Rus, Vladimir Braverman, Dan Feldman
ICML 2023
paper |
abstract |
bibtex |
code
Radial basis function neural networks (RBFNN) are well-known for their capability to approximate any continuous function on a closed bounded set with arbitrary precision given enough hidden neurons. In this paper, we introduce the first algorithm to construct coresets for RBFNNs, i.e., small weighted subsets that approximate the loss of the input data on any radial basis function network and thus approximate any function defined by an RBFNN on the larger input data. In particular, we construct coresets for radial basis and Laplacian loss functions. We then use our coresets to obtain a provable data subset selection algorithm for training deep neural networks. Since our coresets approximate every function, they also approximate the gradient of each weight in a neural network, which is a particular function on the input. We then perform empirical evaluations on function approximation and dataset subset selection on popular network architectures and data sets, demonstrating the efficacy and accuracy of our coreset construction.
@article{tukan2023provable,
title={Provable Data Subset Selection
For Efficient Neural Network Training},
author={Tukan, Murad and Zhou, Samson and Maalouf, Alaa and
Rus, Daniela and Braverman, Vladimir and Feldman, Dan},
journal={arXiv preprint arXiv:2303.05151},
year={2023}
}
|
|
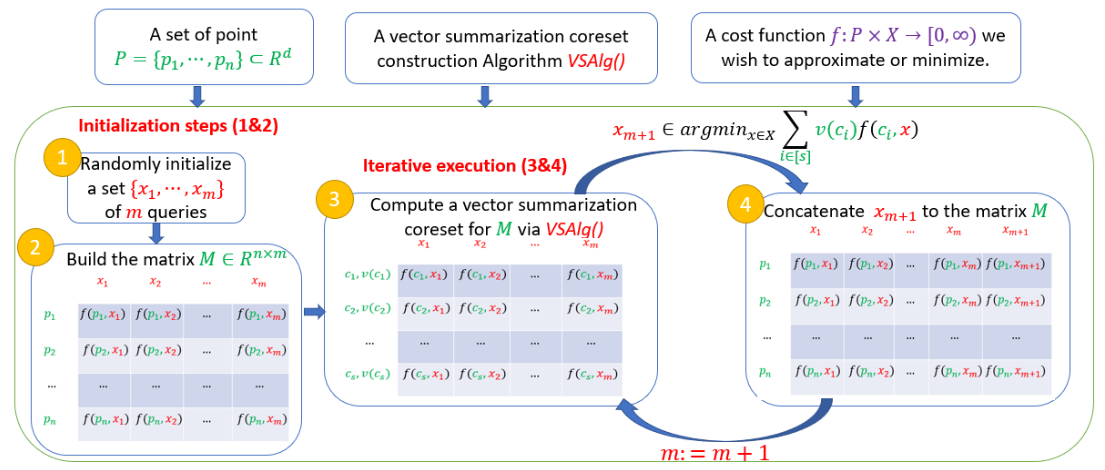
AutoCoreset: An Automatic Practical Coreset Construction Framework
Alaa Maalouf, Murad Tukan, Vladimir Braverman, Daniela Rus
ICML 2023
paper |
abstract |
bibtex |
code
A coreset is a small weighted subset of an input set that approximates its loss function, for a given set of queries. Coresets became prevalent in machine learning as they have shown to be advantageous for many applications. Unfortunately, coresets are constructed in a problem-dependent manner, where for each problem, a new coreset construction algorithm is suggested, taking years to prove its correctness. Even the generic frameworks require additional (problem-dependent) computations or proofs to be done by the user. Besides, many problems do not have (provable) small coresets, limiting their applicability. To this end, we suggest an automatic practical framework for constructing coresets, which requires (only) the input data and the desired cost function from the user, without the need for any other task-related computation to be done by the user. To do so, we reduce the problem of approximating a loss function to an instance of vector summation approximation, where the vectors we aim to sum are loss vectors of a specific subset of the queries, such that we aim to approximate the image of the function on this subset. We show that while this set is limited, the coreset is quite general. An extensive experimental study on various machine learning applications is also conducted. Finally, we provide a ``plug and play" style implementation, proposing a user-friendly system that can be easily used to apply coresets for many problems. We believe that these contributions enable future research and easier use and applications of coresets.
@article{maalouf2023autocoreset,
title={AutoCoreset: An Automatic Practical Coreset
Construction Framework},
author={Maalouf, Alaa and Tukan, Murad and
Braverman, Vladimir and Rus, Daniela},
journal={arXiv preprint arXiv:2305.11980},
year={2023}
}
|
|
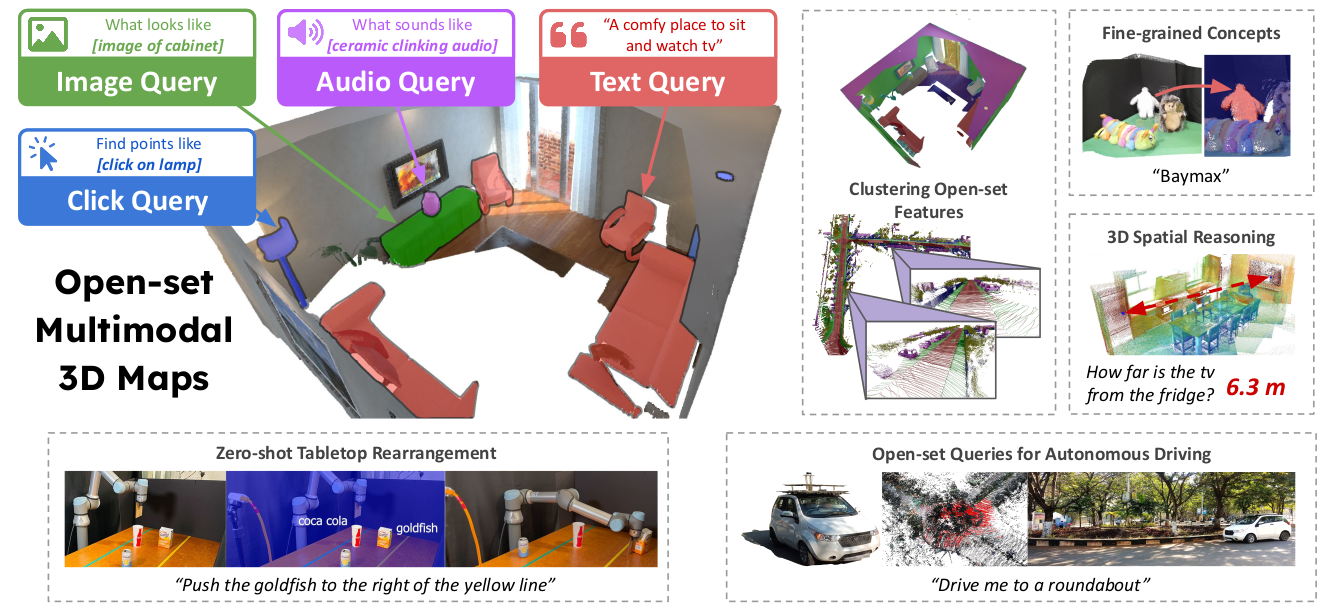
Conceptfusion: Open-set multimodal 3d mapping
Krishna Murthy Jatavallabhula, Alihusein Kuwajerwala, Qiao Gu, Mohd Omama, Tao Chen, Alaa Maalouf, Shuang Li, Ganesh Iyer, Soroush Saryazdi, Nikhil Keetha, Ayush Tewari, Joshua B Tenenbaum, Celso Miguel de Melo, Madhava Krishna, Liam Paull, Florian Shkurti, Antonio Torralba
RSS 2023
paper |
webpage |
abstract |
bibtex |
code
Building 3D maps of the environment is central to robot navigation, planning, and interaction with objects in a scene. Most existing approaches that integrate semantic concepts with 3D maps largely remain confined to the closed-set setting: they can only reason about a finite set of concepts, pre-defined at training time. To address this issue, we propose ConceptFusion, a scene representation that is: (i) fundamentally open-set, enabling reasoning beyond a closed set of concepts (ii) inherently multi-modal, enabling a diverse range of possible queries to the 3D map, from language, to images, to audio, to 3D geometry, all working in concert. ConceptFusion leverages the open-set capabilities of today’s foundation models that have been pre-trained on internet-scale data to reason about concepts across modalities such as natural language, images, and audio. We demonstrate that pixel-aligned open-set features can be fused into 3D maps via traditional SLAM and multi-view fusion approaches. This enables effective zero-shot spatial reasoning, not needing any additional training or finetuning, and retains long-tailed concepts better than supervised approaches, outperforming them by more than 40% margin on 3D IoU. We extensively evaluate ConceptFusion on a number of real-world datasets, simulated home environments, a real-world tabletop manipulation task, and an autonomous driving platform. We showcase new avenues for blending foundation models with 3D open-set multimodal mapping.
@article{jatavallabhula2023conceptfusion,
title={Conceptfusion: Open-set multimodal 3d mapping},
author={Jatavallabhula, Krishna Murthy and Kuwajerwala, Alihusein and
Gu, Qiao and Omama, Mohd and Chen, Tao and Li, Shuang and
Iyer, Ganesh and Saryazdi, Soroush and
Keetha, Nikhil and Tewari, Ayush and others},
journal={arXiv preprint arXiv:2302.07241},
year={2023}
}
|
|
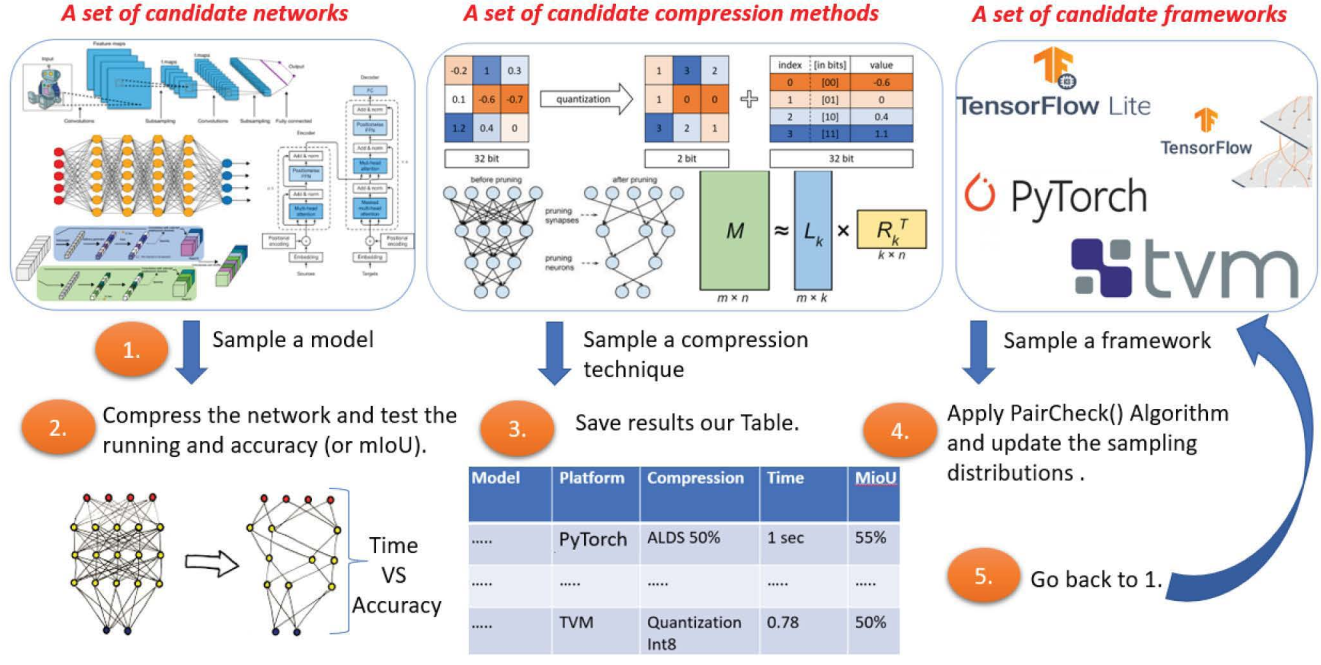
Deep Learning on Home Drone: Searching for the Optimal Architecture
Alaa Maalouf, Yotam Gurfinkel, Barak Diker, Oren Gal, Daniela Rus, and Dan Feldman
ICRA 2023
paper |
abstract |
bibtex |
code
We suggest the first system that runs real-time semantic segmentation via deep learning on a weak micro-computer such as the Raspberry Pi Zero v2 (whose price was $15) attached to a toy-drone. In particular, since the Raspberry Pi weighs less than 16 grams, and its size is half of a credit card, we could easily attach it to the common commercial DJI Tello toy-drone (<$100, <90 grams, 98 × 92.5 × 41 mm). The result is an autonomous drone (no laptop nor human in the loop) that can detect and classify objects in real-time from a video stream of an on-board monocular RGB camera (no GPS or LIDAR sensors). The companion videos demonstrate how this Tello drone scans the lab for people (e.g. for the use of firefighters or security forces) and for an empty parking slot outside the lab. Existing deep learning solutions are either much too slow for real-time computation on such IoT devices, or provide results of impractical quality. Our main challenge was to design a system that takes the best of all worlds among numerous combinations of networks, deep learning platforms/frameworks, compression techniques, and compression ratios. To this end, we provide an efficient searching algorithm that aims to find the optimal combination which results in the best tradeoff between the network running time and its accuracy/performance.
@inproceedings{maalouf2023deep,
title={Deep Learning on Home Drone: Searching for the Optimal Architecture},
author={Maalouf, Alaa and Gurfinkel, Yotam and Diker, Barak and Gal, Oren and Rus, Daniela and Feldman, Dan},
booktitle={2023 IEEE International Conference on Robotics and Automation (ICRA)},
pages={8208--8215},
year={2023},
organization={IEEE}
}
|
| 2022 |
|
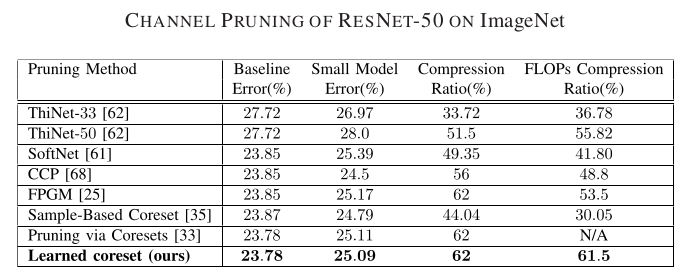
A Unified Approach to Coreset Learning
Alaa Maalouf, Gilad Eini, Ben Mussay, Dan Feldman, Margarita Osadchy
IEEE Transactions on Neural Networks and Learning Systems 2022
paper |
abstract |
bibtex |
code
Coreset of a given dataset and loss function is usually a small weighed set that approximates this loss for every query from a given set of queries. Coresets have shown to be very useful in many applications. However, coresets’ construction is done in a problem-dependent manner and it could take years to design and prove the correctness of a coreset for a specific family of queries. This could limit coresets’ use in practical applications. Moreover, small coresets provably do not exist for many problems. To address these limitations, we propose a generic, learning-based algorithm for construction of coresets. Our approach offers a new definition of coreset, which is a natural relaxation of the standard definition and aims at approximating the average loss of the original data over the queries. This allows us to use a learning paradigm to compute a small coreset of a given set of inputs with respect to a given loss function using a training set of queries. We derive formal guarantees for the proposed approach. Experimental evaluation on deep networks and classic machine learning problems show that our learned coresets yield comparable or even better results than the existing algorithms with worst case theoretical guarantees (that may be too pessimistic in practice). Furthermore, our approach applied to deep network pruning provides the first coreset for a full deep network, i.e., compresses all the networks at once, and not layer by layer or similar divide-and-conquer methods.
@article{maalouf2022unified,
title={A unified approach to coreset learning},
author={Maalouf, Alaa and Eini, Gilad and Mussay, Ben and
Feldman, Dan and Osadchy, Margarita},
journal={IEEE Transactions on Neural Networks and Learning Systems},
year={2022},
publisher={IEEE}
}
|
|
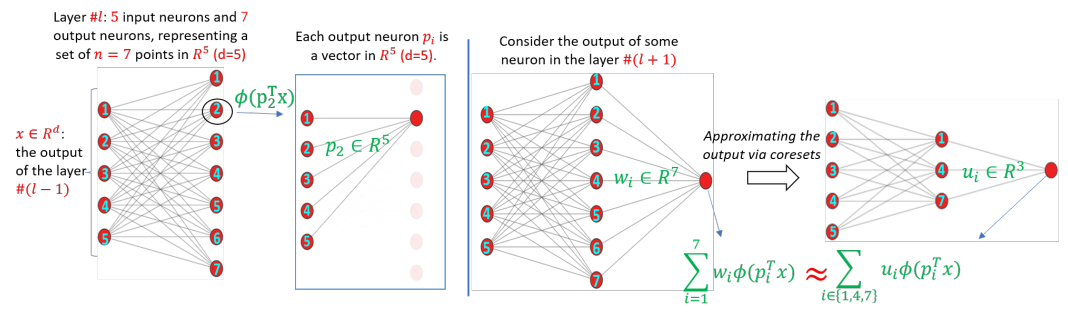
Pruning Neural Networks via Coresets and Convex Geometry: Towards No Assumptions
Murad Tukan, Loay Mualem, Alaa Maalouf,
NeurIPS 2022
paper |
abstract |
bibtex
Pruning is one of the predominant approaches for compressing deep neural networks (DNNs). Lately, coresets (provable data summarizations) were leveraged for pruning DNNs, adding the advantage of theoretical guarantees on the trade-off between the compression rate and the approximation error. However, coresets in this domain were either data dependant or generated under restrictive assumptions on both the model's weights and inputs. In real-world scenarios, such assumptions are rarely satisfied, limiting the applicability of coresets. To this end, we suggest a novel and robust framework for computing such coresets under mild assumptions on the model's weights and without any assumption on the training data. The idea is to compute the importance of each neuron in each layer with respect to the output of the following layer. This is achieved by an elegant combination of L\"{o}wner ellipsoid and Caratheodory theorem.Our method is simultaneously data-independent, applicable to various networks and datasets (due to the simplified assumptions), and theoretically supported. Experimental results show that our method outperforms existing coreset based neural pruning approaches across a wide range of networks and datasets. For example, our method achieved a 62% compression rate on ResNet50 on ImageNet with 1.09% drop in accuracy.
@article{tukan2022pruning,
title={Pruning neural networks via coresets and
convex geometry: Towards no assumptions},
author={Tukan, Murad and Mualem, Loay and Maalouf, Alaa},
journal={Advances in Neural Information Processing Systems},
volume={35},
pages={38003--38019},
year={2022}
}
|
|
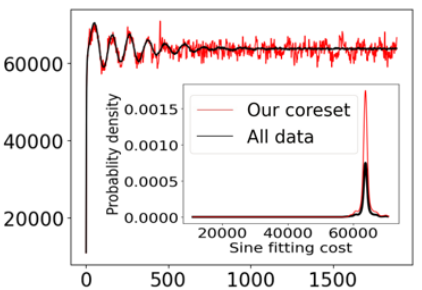
Coresets for Data Discretization and Sine Wave Fitting
Alaa Maalouf, Murad Tukan, Eric Price, Daniel M. Kane, Dan Feldman
AIStats 2022
paper |
abstract |
bibtex |
code
In the monitoring problem, the input is an unbounded stream P=p1,p2⋯ of integers in [N]:={1,⋯,N}, that are obtained from a sensor (such as GPS or heart beats of a human). The goal (e.g., for anomaly detection) is to approximate the n points received so far in P by a single frequency sin, e.g. minc∈Ccost(P,c)+λ(c), where cost(P,c)=∑ni=1sin2(2πNpic), C⊆[N] is a feasible set of solutions, and λ is a given regularization function. For any approximation error ε>0, we prove that every set P of n integers has a weighted subset S⊆P (sometimes called core-set) of cardinality |S|∈O(log(N)O(1)) that approximates cost(P,c) (for every c∈[N]) up to a multiplicative factor of 1±ε. Using known coreset techniques, this implies streaming algorithms using only O((log(N)log(n))O(1)) memory. Our results hold for a large family of functions. Experimental results and open source code are provided.
@inproceedings{maalouf2022coresets,
title={Coresets for data discretization and sine wave fitting},
author={Maalouf, Alaa and Tukan, Murad and Price, Eric and
Kane, Daniel M and Feldman, Dan},
booktitle={International Conference on Artificial
Intelligence and Statistics},
pages={10622--10639},
year={2022},
organization={PMLR}
}
|
|
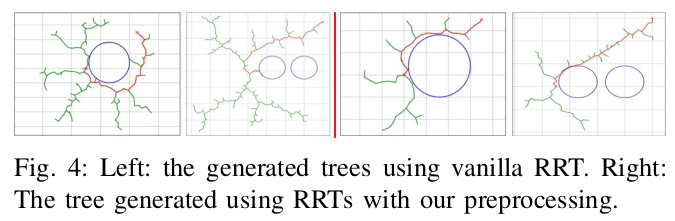
Obstacle Aware Sampling for Path Planning
Murad Tukan, Alaa Maalouf, Dan Feldman, Roi Poranne
IROS 2022
paper |
abstract |
bibtex
Many path planning algorithms are based on sampling the state space. While this approach is very simple, it can become costly when the obstacles are unknown, since samples hitting these obstacles are wasted. The goal of this paper is to efficiently identify obstacles in a map and remove them from the sampling space. To this end, we propose a pre-processing algorithm for space exploration that enables more efficient sampling. We show that it can boost the performance of other space sampling methods and path planners. Our approach is based on the fact that a convex obstacle can be approximated provably well by its minimum volume enclosing ellipsoid (MVEE), and a non-convex obstacle may be partitioned into convex shapes. Our main contribution is an al-gorithm that strategically finds a small sample, called the active-coreset, that adaptively samples the space via membership-oracle such that the MVEE of the coreset approximates the MVEE of the obstacle. Experimental results confirm the ef-fectiveness of our approach across multiple planners based on rapidly-exploring random trees, showing significant improve-ment in terms of time and path length.
@inproceedings{tukan2022obstacle,
title={Obstacle aware sampling for path planning},
author={Tukan, Murad and Maalouf, Alaa and
Feldman, Dan and Poranne, Roi},
booktitle={2022 IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS)},
pages={13676--13683},
year={2022},
organization={IEEE}
}
|
|
Fast and Accurate Least-Mean-Squares Solvers for High Dimensional Data
Alaa Maalouf, Ibrahim Jubran, Dan Feldman
TPAMI 2022
paper |
abstract |
bibtex |
code
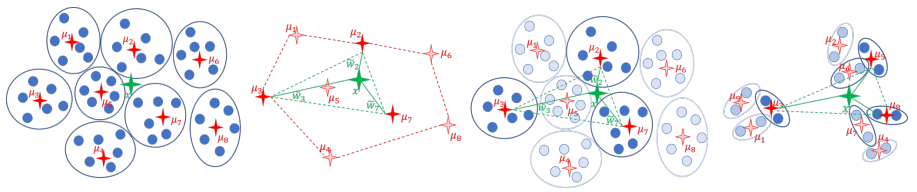
Least-mean-squares (LMS) solvers such as Linear / Ridge-Regression and SVD not only solve fundamental machine learning problems, but are also the building blocks in a variety of other methods, such as matrix factorizations. We suggest an algorithm that gets a finite set of n d -dimensional real vectors and returns a subset of d+1 vectors with positive weights whose weighted sum is exactly the same. The constructive proof in Caratheodory's Theorem computes such a subset in O(n2d2) time and thus not used in practice. Our algorithm computes this subset in O(nd+d4logn) time, using O(logn) calls to Caratheodory's construction on small but “smart” subsets. This is based on a novel paradigm of fusion between different data summarization techniques, known as sketches and coresets. For large values of d , we suggest a faster construction that takes O(nd) time and returns a weighted subset of O(d) sparsified input points. Here, a sparsified point means that some of its entries were set to zero. As an application, we show how to boost the performance of existing LMS solvers, such as those in scikit-learn library, up to x100. Generalization for streaming and distributed data is trivial. Extensive experimental results and open source code are provided.
@article{maalouf2022fast,
title={Fast and accurate least-mean-squares solvers
for high dimensional data},
author={Maalouf, Alaa and Jubran, Ibrahim and Feldman, Dan},
journal={IEEE Transactions on Pattern Analysis
and Machine Intelligence},
volume={44},
number={12},
pages={9977--9994},
year={2022},
publisher={IEEE}
}
|
| 2021 |
|
Compressing Neural Networks: Towards Determining the Optimal Layer-wise Decomposition
Lucas Liebenwein, Alaa Maalouf, Dan Feldman, Daniela Rus
NeurIPS 2021
paper |
abstract |
bibtex |
code
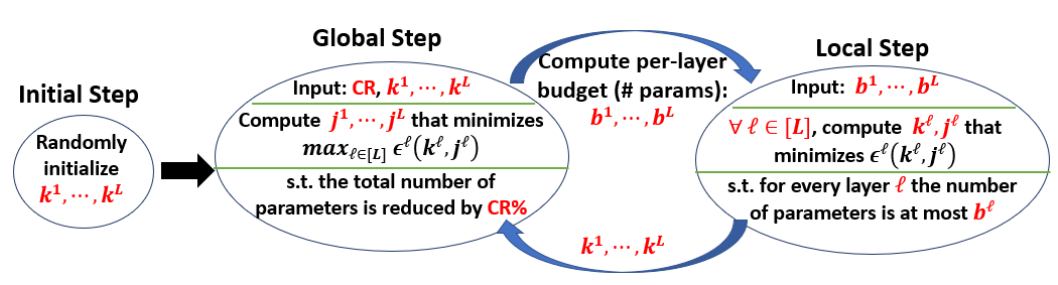
We present a novel global compression framework for deep neural networks that automatically analyzes each layer to identify the optimal per-layer compression ratio, while simultaneously achieving the desired overall compression. Our algorithm hinges on the idea of compressing each convolutional (or fully-connected) layer by slicing its channels into multiple groups and decomposing each group via low-rank decomposition. At the core of our algorithm is the derivation of layer-wise error bounds from the Eckart–Young–Mirsky theorem. We then leverage these bounds to frame the compression problem as an optimization problem where we wish to minimize the maximum compression error across layers and propose an efficient algorithm towards a solution. Our experiments indicate that our method outperforms existing low-rank compression approaches across a wide range of networks and data sets. We believe that our results open up new avenues for future research into the global performance-size trade-offs of modern neural networks.
@article{liebenwein2021compressing,
title={Compressing neural networks:
Towards determining the optimal layer-wise decomposition},
author={Liebenwein, Lucas and Maalouf, Alaa and
Feldman, Dan and Rus, Daniela},
journal={Advances in Neural Information Processing Systems},
volume={34},
pages={5328--5344},
year={2021}
}
|
|
Provably Approximated Point Cloud Registration
Ibrahim Jubran, Alaa Maalouf, Ron Kimmel, Dan Feldman
ICCV 2021
paper |
abstract |
bibtex |
code
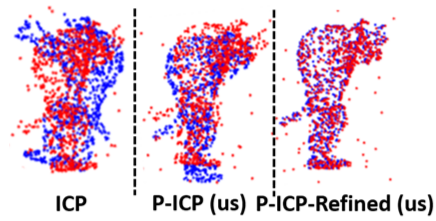
The goal of the alignment problem is to align a (given) point cloud P = \ p_1,\cdots,p_n\ to another (observed) point cloud Q = \ q_1,\cdots,q_n\ . That is, to compute a rotation matrix R \in \mathbb R ^ 3 x3 and a translation vector t \in \mathbb R ^ 3 that minimize the sum of paired distances between every transformed point Rp_i-t, to its corresponding point q_i, over every i\in \br 1,\cdots,n . A harder version is the registration problem, where the correspondence is unknown, and the minimum is also over all possible correspondence functions from P to Q. Algorithms such as the Iterative Closest Point (ICP) and its variants were suggested for these problems, but none yield a provable non-trivial approximation for the global optimum. We prove that there always exists a "witness" set of 3 pairs in P xQ that, via novel alignment algorithm, defines a constant factor approximation (in the worst case) to this global optimum. We then provide algorithms that recover this witness set and yield the first provable constant factor approximation for the: (i) alignment problem in O(n) expected time, and (ii) registration problem in polynomial time. Such small witness sets exist for many variants including points in d-dimensional space, outlier-resistant cost functions, and different correspondence types. Extensive experimental results on real and synthetic datasets show that, in practice, our approximation constants are close to 1 and our error is up to x10 times smaller than state-of-the-art algorithms.
@inproceedings{jubran2021provably,
title={Provably approximated point cloud registration},
author={Jubran, Ibrahim and
Maalouf, Alaa and Kimmel, Ron and Feldman, Dan},
booktitle={Proceedings of the IEEE/CVF
International Conference on Computer Vision},
pages={13269--13278},
year={2021}
}
|
|
Coresets for the Average Case Error for Finite Query Sets
Alaa Maalouf, Ibrahim Jubran, Murad Tukan ,Dan Feldman
MDPI Sensors 2021
paper |
abstract |
bibtex |
code
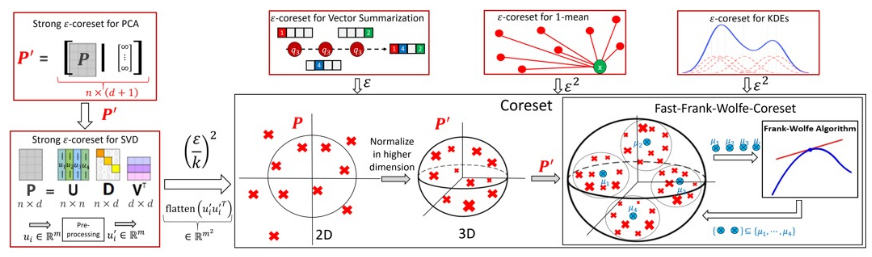
Coreset is usually a small weighted subset of an input set of items, that provably approximates their loss function for a given set of queries (models, classifiers, hypothesis). That is, the maximum (worst-case) error over all queries is bounded. To obtain smaller coresets, we suggest a natural relaxation: coresets whose average error over the given set of queries is bounded. We provide both deterministic and randomized (generic) algorithms for computing such a coreset for any finite set of queries. Unlike most corresponding coresets for the worst-case error, the size of the coreset in this work is independent of both the input size and its Vapnik–Chervonenkis (VC) dimension. The main technique is to reduce the average-case coreset into the vector summarization problem, where the goal is to compute a weighted subset of the n input vectors which approximates their sum. We then suggest the first algorithm for computing this weighted subset in time that is linear in the input size, for 𝑛≫1/𝜀, where 𝜀 is the approximation error, improving, e.g., both [ICML’17] and applications for principal component analysis (PCA) [NIPS’16]. Experimental results show significant and consistent improvement also in practice. Open source code is provided.
@article{maalouf2021coresets,
title={Coresets for the average case error for finite query sets},
author={Maalouf, Alaa and Jubran, Ibrahim and
Tukan, Murad and Feldman, Dan},
journal={Sensors},
volume={21},
number={19},
pages={6689},
year={2021},
publisher={MDPI}
}
|
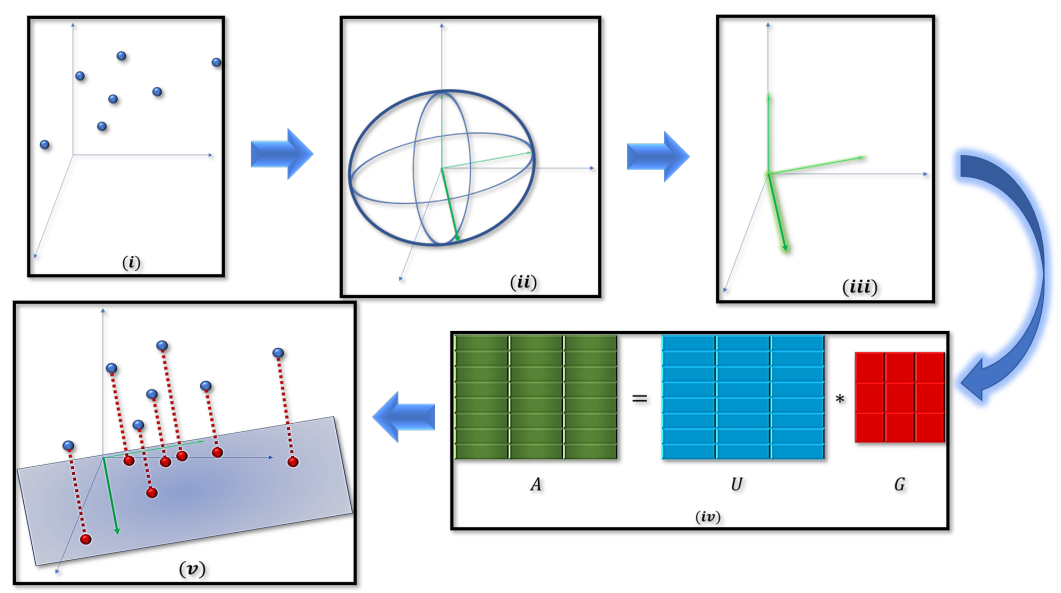
|
No fine-tuning, no cry: Robust svd for compressing deep networks
Murad Tukan Alaa Maalouf, Matan Weksler, Dan Feldman
MDPI Sensors 2021
paper |
abstract |
bibtex |
code
A common technique for compressing a neural network is to compute the k-rank ℓ2 approximation 𝐴𝑘 of the matrix 𝐴∈ℝ𝑛×𝑑 via SVD that corresponds to a fully connected layer (or embedding layer). Here, d is the number of input neurons in the layer, n is the number in the next one, and 𝐴𝑘 is stored in 𝑂((𝑛+𝑑)𝑘) memory instead of 𝑂(𝑛𝑑). Then, a fine-tuning step is used to improve this initial compression. However, end users may not have the required computation resources, time, or budget to run this fine-tuning stage. Furthermore, the original training set may not be available. In this paper, we provide an algorithm for compressing neural networks using a similar initial compression time (to common techniques) but without the fine-tuning step. The main idea is replacing the k-rank ℓ2 approximation with ℓ𝑝, for 𝑝∈[1,2], which is known to be less sensitive to outliers but much harder to compute. Our main technical result is a practical and provable approximation algorithm to compute it for any 𝑝≥1, based on modern techniques in computational geometry. Extensive experimental results on the GLUE benchmark for compressing the networks BERT, DistilBERT, XLNet, and RoBERTa confirm this theoretical advantage.
@article{tukan2021no,
title={No fine-tuning, no cry: Robust svd for compressing deep networks},
author={Tukan, Murad and Maalouf, Alaa and Weksler, Matan and Feldman, Dan},
journal={Sensors},
volume={21},
number={16},
pages={5599},
year={2021},
publisher={MDPI}
}
|
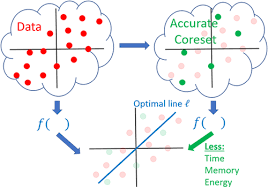
|
Overview of accurate coresets
Ibrahim Jubran Alaa Maalouf, Dan Feldman
Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 2021
paper |
abstract |
bibtex |
code
A coreset of an input set is its small summarization, such that solving a problem on the coreset as its input, provably yields the same result as solving the same problem on the original (full) set, for a given family of problems (models/classifiers/loss functions). Coresets have been suggested for many fundamental problems, for example, in machine/deep learning, computer vision, databases, and theoretical computer science. This introductory paper was written following requests regarding the many inconsistent coreset definitions, lack of source code, the required deep theoretical background from different fields, and the dense papers that make it hard for beginners to apply and develop coresets. The article provides folklore, classic, and simple results including step-by-step proofs and figures, for the simplest (accurate) coresets. Nevertheless, we did not find most of their constructions in the literature. Moreover, we expect that putting them together in a retrospective context would help the reader to grasp current results that usually generalize these fundamental observations. Experts might appreciate the unified notation and comparison table for existing results. Open source code is provided for all presented algorithms, to demonstrate their usage, and to support the readers who are more familiar with programming than mathematics.
@article{jubran2021overview,
title={Overview of accurate coresets},
author={Jubran, Ibrahim and Maalouf, Alaa and Feldman, Dan},
journal={Wiley Interdisciplinary Reviews:
Data Mining and Knowledge Discovery},
volume={11},
number={6},
pages={e1429},
year={2021},
publisher={Wiley Online Library}
}
|
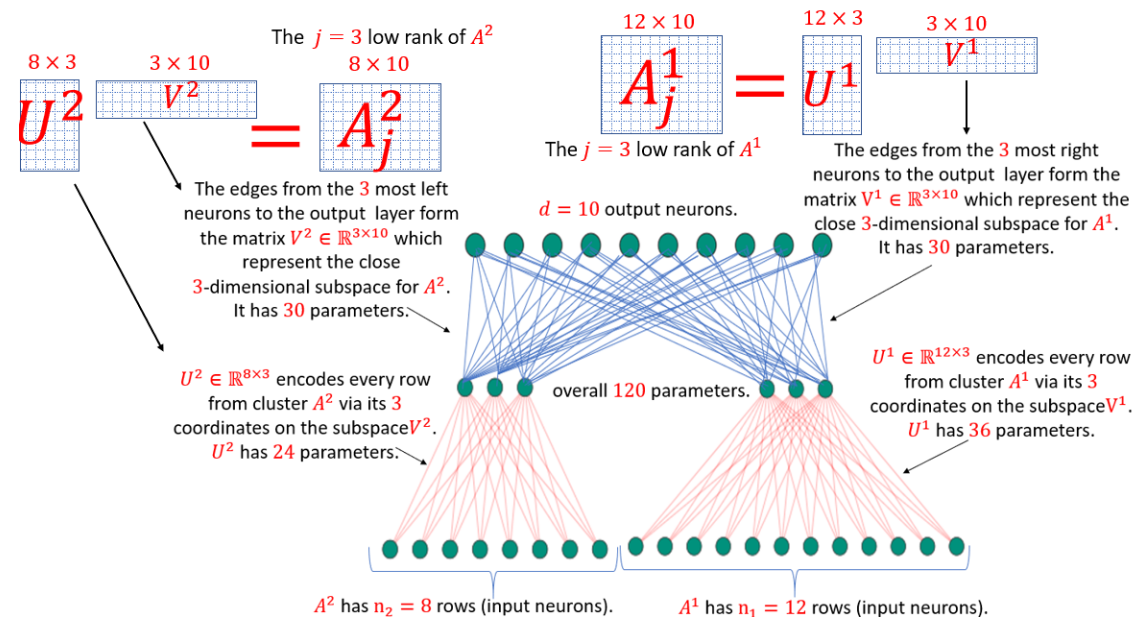
|
Deep Learning Meets Projective Clustering
Alaa Maalouf, Hary Lang, Daniela Rus, Dan Feldman
ICLR 2021
paper |
abstract |
bibtex |
code
A common approach for compressing NLP networks is to encode the embedding layer as a matrix A∈Rn×d, compute its rank-j approximation Aj via SVD, and then factor Aj into a pair of matrices that correspond to smaller fully-connected layers to replace the original embedding layer. Geometrically, the rows of A represent points in Rd, and the rows of Aj represent their projections onto the j-dimensional subspace that minimizes the sum of squared distances ("errors") to the points. In practice, these rows of A may be spread around k>1 subspaces, so factoring A based on a single subspace may lead to large errors that turn into large drops in accuracy. Inspired by \emph{projective clustering} from computational geometry, we suggest replacing this subspace by a set of k subspaces, each of dimension j, that minimizes the sum of squared distances over every point (row in A) to its \emph{closest} subspace. Based on this approach, we provide a novel architecture that replaces the original embedding layer by a set of k small layers that operate in parallel and are then recombined with a single fully-connected layer. Extensive experimental results on the GLUE benchmark yield networks that are both more accurate and smaller compared to the standard matrix factorization (SVD). For example, we further compress DistilBERT by reducing the size of the embedding layer by 40% while incurring only a 0.5% average drop in accuracy over all nine GLUE tasks, compared to a 2.8% drop using the existing SVD approach. On RoBERTa we achieve 43% compression of the embedding layer with less than a 0.8% average drop in accuracy as compared to a 3% drop previously. Open code for reproducing and extending our results is provided.
@inproceedings{
maalouf2021deep,
title={Deep Learning meets Projective Clustering},
author={Alaa Maalouf and Harry Lang and Daniela Rus and Dan Feldman},
booktitle={International Conference on Learning Representations},
year={2021},
url={https://openreview.net/forum?id=EQfpYwF3-b}
}
|
| 2020 |
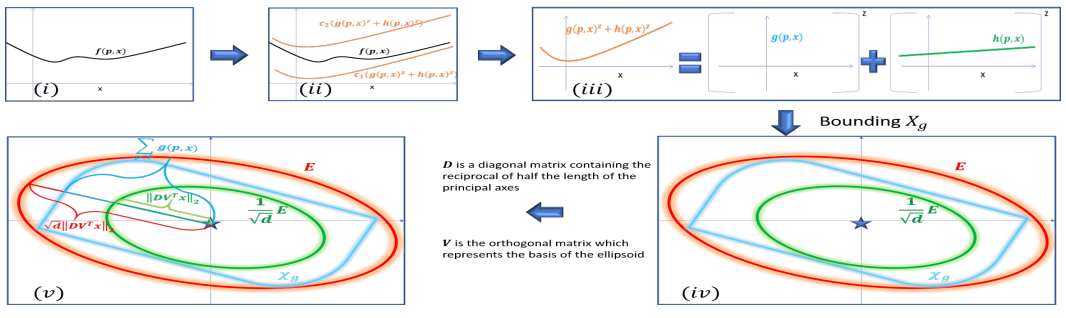
|
Coresets for Near-Convex Functions
Murad Tukan, Alaa Maalouf, Dan Feldman
NeurIPS 2020
paper |
abstract |
bibtex |
Coreset is usually a small weighted subset of n input points in Rd, that provably approximates their loss function for a given set of queries (models, classifiers, etc.). Coresets become increasingly common in machine learning since existing heuristics or inefficient algorithms may be improved by running them possibly many times on the small coreset that can be maintained for streaming distributed data. Coresets can be obtained by sensitivity (importance) sampling, where its size is proportional to the total sum of sensitivities. Unfortunately, computing the sensitivity of each point is problem dependent and may be harder to compute than the original optimization problem at hand. We suggest a generic framework for computing sensitivities (and thus coresets) for wide family of loss functions which we call near-convex functions. This is by suggesting the f-SVD factorization that generalizes the SVD factorization of matrices to functions. Example applications include coresets that are either new or significantly improves previous results, such as SVM, Logistic regression, M-estimators, and ℓz-regression. Experimental results and open source are also provided.
@article{tukan2020coresets,
title={Coresets for near-convex functions},
author={Tukan, Murad and Maalouf, Alaa and Feldman, Dan},
journal={Advances in Neural Information Processing Systems},
volume={33},
pages={997--1009},
year={2020}
}
|
|
Sets Clustering
Ibrahim Hubran, Murad Tukan, Alaa Maalouf, Dan Feldman
ICML 2020
paper |
abstract |
bibtex |
code
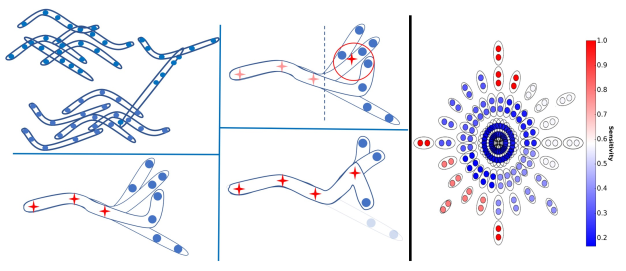
The input to the \emph{sets-k-means} problem is an integer k≥1 and a set P={P1,⋯,Pn} of fixed sized sets in Rd. The goal is to compute a set C of k centers (points) in Rd that minimizes the sum ∑P∈Pminp∈P,c∈C∥p−c∥2 of squared distances to these sets. An \emph{ε-core-set} for this problem is a weighted subset of P that approximates this sum up to 1±ε factor, for \emph{every} set C of k centers in Rd. We prove that such a core-set of O(log2n) sets always exists, and can be computed in O(nlogn) time, for every input P and every fixed d,k≥1 and ε∈(0,1). The result easily generalized for any metric space, distances to the power of z>0, and M-estimators that handle outliers. Applying an inefficient but optimal algorithm on this coreset allows us to obtain the first PTAS (1+ε approximation) for the sets-k-means problem that takes time near linear in n. This is the first result even for sets-mean on the plane (k=1, d=2). Open source code and experimental results for document classification and facility locations are also provided.
@inproceedings{jubran2020sets,
title={Sets clustering},
author={Jubran, Ibrahim and Tukan, Murad and Maalouf, Alaa and Feldman, Dan},
booktitle={International Conference on Machine Learning},
pages={4994--5005},
year={2020},
organization={PMLR}
}
|
|
Tight sensitivity bounds for smaller coresets
Alaa Maalouf, Adiel Statman, Dan Feldman
KDD 2020
paper |
abstract |
bibtex |
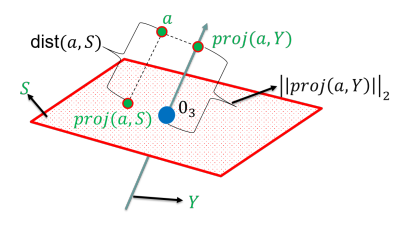
An ε-coreset to the dimensionality reduction problem for a (possibly very large) matrix A ∈ Rn x d is a small scaled subset of its n rows that approximates their sum of squared distances to every affine k-dimensional subspace of Rd, up to a factor of 1±ε. Such a coreset is useful for boosting the running time of computing a low-rank approximation (k-SVD/k-PCA) while using small memory. Coresets are also useful for handling streaming, dynamic and distributed data in parallel. With high probability, non-uniform sampling based on the so called leverage score or sensitivity of each row in A yields a coreset. The size of the (sampled) coreset is then near-linear in the total sum of these sensitivity bounds. We provide algorithms that compute provably tight bounds for the sensitivity of each input row. It is based on two ingredients: (i) iterative algorithm that computes the exact sensitivity of each row up to arbitrary small precision for (non-affine) k-subspaces, and (ii) a general reduction for computing a coreset for affine subspaces, given a coreset for (non-affine) subspaces in Rd. Experimental results on real-world datasets, including the English Wikipedia documents-term matrix, show that our bounds provide significantly smaller and data-dependent coresets also in practice. Full open source code is also provided.
@inproceedings{maalouf2020tight,
title={Tight sensitivity bounds for smaller coresets},
author={Maalouf, Alaa and Statman, Adiel and Feldman, Dan},
booktitle={Proceedings of the 26th ACM SIGKDD international
conference on knowledge discovery \& data mining},
pages={2051--2061},
year={2020}
}
|
| 2019 |

|
Fast and accurate least-mean-squares solvers
Alaa Maalouf, Ibrahim Hubran, Dan Feldman
NeurIPS 2019 (Outstanding Paper Honorable Mention Award)
paper |
abstract |
bibtex |
code
Least-mean squares (LMS) solvers such as Linear / Ridge / Lasso-Regression, SVD and Elastic-Net not only solve fundamental machine learning problems, but are also the building blocks in a variety of other methods, such as decision trees and matrix factorizations. We suggest an algorithm that gets a finite set of n d-dimensional real vectors and returns a weighted subset of d+1 vectors whose sum is exactly the same. The proof in Caratheodory's Theorem (1907) computes such a subset in O(n2d2) time and thus not used in practice. Our algorithm computes this subset in O(nd) time, using O(log(n)) calls to Caratheodory's construction on small but "smart" subsets. This is based on a novel paradigm of fusion between different data summarization techniques, known as sketches and coresets. As an example application, we show how it can be used to boost the performance of existing LMS solvers, such as those in scikit-learn library, up to x100. Generalization for streaming and distributed (big) data is trivial. Extensive experimental results and complete open-source code are also provided.
@article{maalouf2019fast,
title={Fast and accurate least-mean-squares solvers},
author={Maalouf, Alaa and Jubran, Ibrahim and Feldman, Dan},
journal={Advances in Neural Information Processing Systems},
volume={32},
year={2019}
}
|
|
Service
- Reviewer: ICML, NeurIPS, CVPR, AAAI, IROS, ICRA, SIGGRAPH, and the Machine Learning Journal.
|
A huge thanks to template from this.
|
|